Science Skool - Redox Reactions

Redox Reactions

You are full of redox reactions. The redox reaction respiration releases the energy you need to live, and the food you eat ultimately comes from the redox reaction photosynthesis. Around you, mobile and laptop batteries work using redox reactions, as do fuel cells, bleaches, old fashioned wet photography, and metal corrosion, such as rusting iron.

So what are redox reactions?

The word redox comes from two words: Reduction and Oxidation. In a reaction, oxidation is the loss of electrons from an atom or ion, and reduction is the gain of electrons by an atom or ion. In a redox reaction there is the gain of electrons by one chemical, reduction, and the loss of electrons by another chemical, oxidation, so both are found together. You must remember

oxidation is the process of electron loss
reduction is the process of electron gain

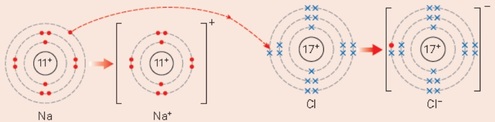
An example of redox is when the metal sodium, reacts with the green gas chlorine and then the white solid sodium chloride is made.

Na(s) + Cl₂(g) --> NaCl(s)

The sodium has been oxidised and the chlorine has been reduced.

Sodium metal is made of sodium atoms. In the reaction, each sodium atom loses an electron to a chlorine atom, so this is called oxidation. The sodium atom starts with the electronic configuration 2,8,1. When it reacts to form a sodium ion (Na+) and because it has lost an electron its electronic configuration is now 2,8.

The chlorine gas is made of chlorine atoms. In the reaction, each chlorine atom gains one electron to form a chloride ion (Cl^-) and this is called reduction. The chlorine atom starts with the electronic configuration 2,8,7. When it reacts to form a chlorine ion it has gained an electron so its electronic configuration is now 2,8,8.

Ancient reduction

You may wonder why the word reduction is used to mean a gain of electrons. Thousands of years ago it was noticed that the metal made by smelting had less mass than the original ore. The ore was made smaller, reduced. The loss of oxygen made the mass less. More recently it was realised that the metal atoms were gaining electrons.

Copper ore is reduced to copper metal. The copper metal has less mass than the copper ore. The copper ions have gained electrons. In this example reduction means “make smaller” and “gain of electrons”.

Oxidising agents and reducing agents

Oxidising agents oxidise other chemicals, so oxidising agents are themselves reduced, so oxidising agents gain electrons. Reducing agents reduce other chemicals, so they lose electrons. You must remember that:

oxidising agents are electron acceptors
reducing agents are electron donors

Why oxidation?

Oxidation used to mean just ‘gain of oxygen’, but it was realized, more importantly, that the other chemical was losing electrons to the oxygen. So it was decided that ‘oxidation’ should have the broader meaning ‘loss of electrons’.

The Thermite reaction

To allow trains to travel at high speeds the rails must be welded together so there are no gaps. This must be done in isolated places so molten iron is made using the thermite reaction:

Fe₂O₃(s) + Al(s) --> Al₂O₃(s) + Fe(l)

Here the iron (III) oxide, Fe₂O₃, is reduced to iron, Fe:

the iron(III) oxide is reduced
the iron(III) oxide is the oxidizing agent

The aluminium powder, Al, is oxidized to aluminium oxide, Al₂O₃:

the aluminium is oxidized

The aluminium is the reducing agent

Half equations

What are half-equations? Half equations show the gain or loss of electrons by one chemical. For example, this is the full equation for when sodium reacts with chlorine:

2Na(s) + Cl₂(g) -->2NaCl(s)

Each sodium atom is losing an electron to a chlorine atom (it is being oxidised), so you could write this half equation:

Na(s) --> Na⁺(s) + e^-

Each chlorine atom in a chlorine molecule gains an electron (it is being reduced), so you could write this half equation:

Cl₂(g) + 2e^- --> 2Cl^-(g)

(You need to show two chloride ions because each chlorine molecule, Cl2, contains two chlorine atoms.) The way sodium reacts does not depend on the other reactant. For example, if sodium reacted with bromine instead of chlorine the equation would be:

2Na(s) + Br₂(g) -->2NaBr(s)

Sodium is still gaining electrons in the same way; and the half equation for bromine becomes:

Br₂(g) + 2e^- --> 2Br^-(g)

What we have been writing here are known as half equations, but this only shows half the story, either the gain or the loss of electrons. For a full equation we would need to put two halves together (which we will see in a while).

Be aware that some ions are spectator ions and they take no part in the reaction. When zinc is put into copper sulfate solution the full equation is:

Zn(s) + CuSO₄(aq) --> Cu(s) + ZnSO₄(aq)

Each zinc atom is oxidised:

Zn(s) --> Zn²⁺(aq) + e^-

Each copper ion is reduced:

Cu²⁺(aq) + 2e^- --> Cu(s)

Notice that the sulfate ions, SO₄^2-, do not appear in the equations. They do not change during the reaction. They are dissolved in the water, so are just floating around. As they are said to only ‘watch’ the reaction they are called ‘spectator ions’.

What is an oxidation state?

An oxidation state is the number of electrons needed to be gained or lost to make a neutral atom. Using oxidation states is a way of working out how oxidized or reduced something is. It is similar to the charge on ions, except that it is also used for covalent compounds.

Different oxidation states may have different colours. In this test tube are all the oxidation states of vanadium from pale yellow +5 to violet +2 at the bottom. Two oxidation states of manganese produced the colours at the top.

How to Work out Oxidation States

Use these rules to calculate oxidation state:

Elements always have an oxidation state of zero.
In a compound, the sum of the oxidation numbers equals zero.
In an ion, the sum of the oxidation numbers equals the charge.

In a compound:

Group 1 atoms always have a +1 oxidation state, e.g. Na is +1 in NaCl.
Group 2 atoms always have a +2 oxidation state, e.g. Mg is +2 in MgCl₂.
Group 3 atoms always have a +3 oxidation state, e.g. Al is +3 in AlCl₃.
Fluorine always has a –1 oxidation state, e.g. F is –1 in KF.
Oxygen has a –2 oxidation state, unless it is in a peroxide compound, such as H₂O₂, when O is –1, or with fluorine (as F is more electronegative than O); e.g. O is –2 in MgO, but is –1 in Na₂O₂, and +2 in OF₂
Chlorine has a –1 oxidation state, unless it is with F or O (as they are more electronegative than Cl), e.g. Cl is –1 in NaCl, but +1 in Cl₂O, and +3 in ClF₃.
Hydrogen is +1 except in metal hydrides where it has an oxidation state of –1, e.g. H is +1 in HCl, +1 in H₂O, but –1 in NaH.

Oxidation state examples:

Here are some examples of common compounds with all the oxidation numbers:

Sodium Chloride (common salt), NaCl, Na = +1, Cl = –1
Sodium Carbonate (washing soda), Na₂CO₃, Na = +1, C = +4, O = –2
Calcium Fluoride (fluorspar), CaF₂, Ca = +2, F = –1
Calcium Hydroxide (lime water), Ca(OH)₂, Ca = +2, O = –2, H = +1
Calcium Hydroxide (lime water), Ca(OH)₂, Ca = +2, O = –2, H = +1
Potassium Nitrate (saltpetre), KNO₃, K = +1, N = +5, O = –2
Iron(III) Oxide (haematite), Fe₂O₃, Fe = +3, O = –2
Copper(II) Sulfate, CuSO₄, Cu = +2, S = +6, O = –2

How to combine two half-equations

The easiest way to combine two half-equations is to work in steps:

Step 1 Write out the two half-equations.

Step 2 Note the number of electrons each half-equation gains or loses. So that both equations involve the same number of electrons, you may have to multiply up one or both equations. This means the electrons can be cancelled out.

Step 3 Multiply up the reactants and products.

Step 4 Write all the reactants together, and the products together.

Step 5 The equation should now be balanced. In some of the more difficult examples you may need to add H⁺, OH^- or H₂O to one or both of the sides of the equation. This is best explained with an example later.

Our first example could be balanced in the traditional way, but for the purpose of this topic I will show it being balanced using oxidation states and redox.

Example:

Balance this equation:

FeSO₄ + Na --> Na₂SO₄ + Fe

Step1: Add oxidation values

\[\frac{{ + 2}}{{Fe}}\frac{{ + 6}}{S}\frac{{ - 8}}{{O4}}\; + \;\frac{0}{{Na}} \to \frac{{ + 2}}{{Na2}}\frac{{ + 6}}{S}\frac{{ - 8}}{{O4}} + \frac{0}{{Fe}}\]

(Note: each oxygen atom is -2, so if you have four of them it is -8 and each sodium atom is +1, so if you have two of them it is +2)

By looking at the oxidation states of each atom, you can see that Fe has been reduced from +2 to 0 and Na has been oxidised from 0 to +1.

Step 2: Now we can write the two half equations:

Fe²⁺ + 2e^- --> Fe

Na --> Na⁺ + e^-

Step 3: Now we need to balance the two half equations:

Fe²⁺ + 2e^- --> Fe

2Na --> 2Na⁺ + 2e^-

The sodium half equation originally only had one electron, for it to equal the iron half equation we needed to multiply it by two.

Step 4: Now everything is balanced lets reinsert it into the full equation, complete with balancing numbers but while also cancelled out the electrons (because there is two on either side).

FeSO₄ + 2Na --> Na₂SO₄ + Fe

(Note: because there was already Na₂ in the equation there was no need to multiply that by two.)

As you can see the equation is now balanced! As mentioned earlier there was no need to use this method for that question, but if we try this one you can see how it is useful.

Example 2:

Balance this equation:

S^2- + I₂ --> SO4^2- + I^-

Step1: Add oxidation values

\[\frac{{2 - }}{{{S^{2 - }}}}\; + \;\frac{0}{{I2}} \to \frac{{ + 6}}{S}\frac{{ - 8}}{{O4}} + \frac{{ - 1}}{{{I^ - }}}\]

(Note: each oxygen atom is -2, so if you have four of them it is -8)

By looking at the oxidation states of each atom, you can see that I has been reduced from 0 to -1 and S has been oxidised from -2 to +6.

Step 2: Now we can write the two half equations:

I + e^- --> I^-

S^2- --> S + 8e^-

Step 3: Now we need to balance the two half equations:

8I + 8e^- --> 8I^-

S^2- --> S + 8e^-

The iodine half equation originally only had one electron, for it to equal the sulfur half equation we needed to multiply it by eight.

Step 4: Now everything is balanced lets reinsert it into the full equation, complete with balancing numbers but while also cancelled out the electrons (because there is two on either side).

S^2- + 4I₂ --> SO4^2- + 8I^-

(Note: In the original equation it was I₂ so because we had 8I atoms, that is the same as 4I₂)

Step 5: If you look at the now ‘balanced’ equation you will see it is actually NOT balanced, because on the right hand side of the equation there are oxygens, but none on the left! We first need to calculate the charge on either side of the equation:

\[\frac{{ - 2}}{{{S^{2 - }} + {\rm{ }}4{I_2}}} \to \frac{{ - 10}}{{SO{4^{2 - }} + {\rm{ }}8{I^ - }}}\]

You can see that the charges are NOT balanced and for it to be a balanced equation they need to. To balance the charges we can either add H+ or OH- depending on the conditions the reaction was completed in. For A-level chemistry 99% of the time it is in acidic conditions and hence you need to add H⁺. The only time I would use OH^- is if that species was already in the reaction or you are explicitly told to.

So by adding H+ to the right hand side, this give us:

S^2- + 4I₂ --> SO4^2- + 8I^- + 8H⁺

(Note: I have added 8 because I need both sides to have the same charge, so now they both equal -2)

The only thing we can add now is water. Just ensure that when adding the water the hydrogen balance and then if you have completed the previous steps you will hopefully find a fully balanced redox equation:

4H₂O + S^2- + 4I₂ --> SO4^2- + 8I^- + 8H⁺

If this is the first time you have done this, this will probably look very difficult and long, but once you get the hang of it, it doesn’t take too long.