Energetics

Chemical reactions involve:

• the breaking of bonds between atoms
• the making of new bonds between atoms

These processes involve energy exchanges between the reacting system and its surroundings.

Enthalpy is the term used to describe the heat (energy) content of a system. It has the symbol H and is measured in kilojoules. It is only really possible to measure enthalpy changes (delta H, written as ΔH). This can be calculated from measured changes in temperature. Enthalpy change is defined as:

The heat energy change measured under conditions of constant pressure.

In a chemical reaction the enthalpy change is easily calculated by subtracting the (total) enthalpy of the reactants (H_r) from the (total) enthalpy of the products (H_p).

\[{\bf{\Delta }}H = Hp - Hr\]

• Exothermic reactions release heat energy (heat flows from the system to the surroundings). ΔH is always negative, so the value always has a minus sign.
• Endothermic reactions absorb heat energy (heat flows from the surroundings into the system). ΔH is always positive. These changes can be shown on enthalpy change diagrams.

Standard enthalpy change of formation ΔH^⦵_f

This is the enthalpy change when one mole of a compound is formed from its elements in their standard states under standard conditions (298K and 100 kPa). For example, when producing magnesium oxide the standard enthalpy of formation is:

Mg(s) + ¹/₂ O₂(g) --> MgO(s)

ΔH^⦵_f = -602kjmol^-1

Remember that this is for one mole of magnesium oxide and you need to give all state symbols in addition to the temperature at which the enthalpy change is measured (this example is given at standard temp and pressure which denoted by the symbol ^⦵.The formation of one mole of magnesium oxide releases 602kJ of energy to the surroundings but if two moles of magnesium oxide been formed then the amount of energy released would have been 1204kJ.)

Standard enthalpy change of combustion ΔH^⦵_c

This is the enthalpy change when one mole of a substance is completely burned in oxygen under standard conditions (100 kPa and 298 K). For example the standard enthalpy of combustion of ethane is:

C₂H₆(g) + 3¹/₂O₂(g)-->2CO₂(g) + 3H₂O(l)

ΔH^⦵_c = -1560 kjmol^-1

Remember that this is for one mole of ethane and to always include state symbols. When completely burnt in oxygen, one mole of ethane releases 1560kJ of energy into the surroundings.

Calculating the Enthalpy of Reaction

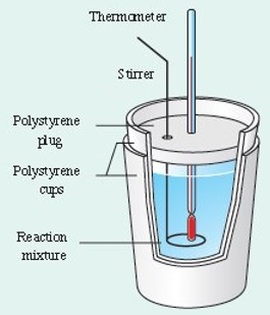
The value of enthalpy changes accompanying chemical reactions can be determined by the use of a calorimeter. The purpose of a calorimeter is to insulate the reaction system from its surroundings. The reaction is carried out in the calorimeter and the change in temperature of the calorimeter is measured. This enables the enthalpy change for the reaction to be determined. There are several types of enthalpy change that can be measured using a calorimeter. These include enthalpy changes of:

• Dissolving
• Neutralisation
• Reactions between acids and bases
• Formation
• Combustion

The heat energy change for any reaction can be calculated using the relationship below:

\[q = mc{\bf{\Delta }}T\]

Where q is the heat energy, m is the mass of substance, c is the specific heat capacity and ΔT is the change in temperature.

Specific heat capacity (c) is the heat energy required to raise the temperature of 1g of a substance by 1K. For pure water the specific heat capacity is 4.18Jg^-1K^-1.

Simple Calorimetry

Two expanded polystyrene cups are placed on inside the other and a wire stirrer is used to ensure thorough mixing. We make the assumption that we have negligible heat loss and that all of the heat exchanged in the reaction is used to alter the temperature of the water.

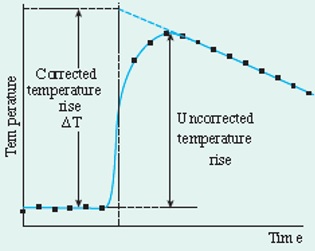
For a reaction carried out in a simple calorimeter if it is assumed that heat loss in the experiment is constant then an accurate figure for the maximum temperature change can be obtained by extrapolation of the graph. Theoretically the maximum temperature should be almost instantaneously after the reactants are mixed, but in real life it takes time for this heat to move through the solution and then affect the thermometer, this extrapolation graph helps negate this problem.

Question on this topic usually revolve around the mathematical application of q=mcΔT. Here is an example question:

A known mass of solid is totally dissolved in a large excess of water whose mass is known. The change in temperature of the water is measured.

In an experiment using a simple calorimeter, 8.00g of ammonium nitrate (NH₄NO₃) was dissolved in 50.0g of water. The temperature fell by 10.1^oC. Calculate the enthalpy change for this process. (The specific heat capacity of water is 4.18JK^-1g^-1. The heat capacity of the container can be ignored.)

Let's attack this step wise:

Step 1: Calculate the heat change from the change in temperature using

q = mass x specific heat capacity of water x change in temperature

\[\begin{array}{l}q = 50.0 \times 4.18 \times 10.1\\q = 2110.9J\end{array}\]

Step 2: Calculate the moles of ammonium nitrate dissolved

\[\begin{array}{l}moles = \frac{{mass}}{{Mr}}\\moles = \frac{{8.0}}{{80}} = 0.10moles\end{array}\]

Step 3: Calculate the enthalpy change per mole of ammonium nitrate

\[\begin{array}{l}\frac{q}{{moles}} = \Delta H\\\frac{{2110.9}}{{0.1}} = 21109Jmo{l^{ - 1}}\end{array}\]

Step 4: Answers are usually given in kJ mol^-1

\[\frac{{21109}}{{1000}} = + 21.109kJmo{l^{ - 1}}\]

The answer should be positive as the temperature decreased! If this was a temperature increase then the enthalpy would be negative.