Time of Flight (TOF) Mass Spectrometer

1. Electrospray Ionisation: The sample is dissolved in a volatile solvent and injected through a fine hollow needle at high pressure. As the solvent evaporates it is subjected to a high voltage which forms positive ions (because it loses electrons).

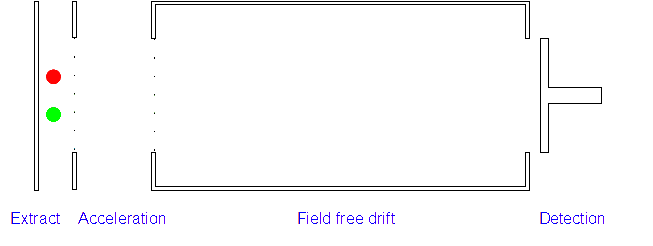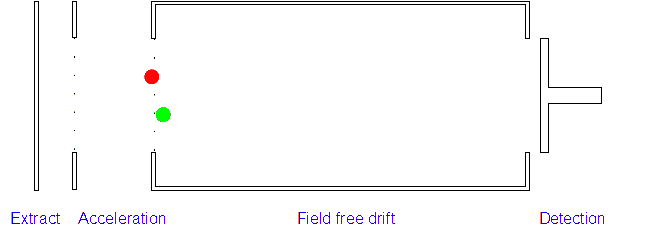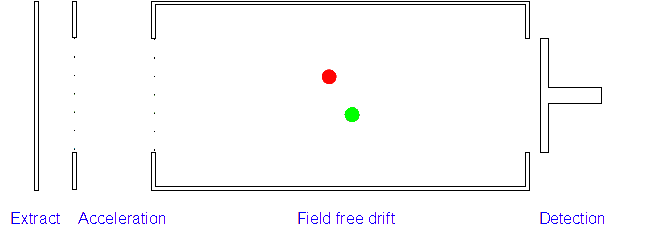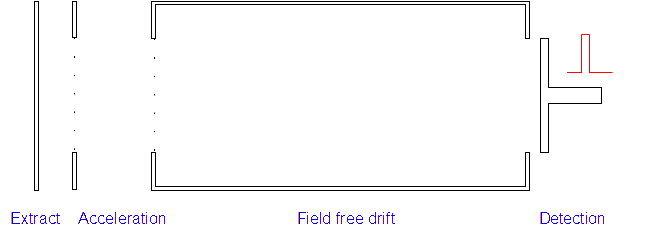
2. Acceleration: The positively charged particles are now accelerated by the electric field which gives each type of ion the same kinetic energy. If the ion has a high mass/charge (m/z) ratio they will be accelerated less than those with low m/z ratios.

3. Ion Drift: The ions leave the electric field and are allowed to drift through it. As their speeds are exactly the same as when first accelerated this will allow them to separate (ions with different m/z ratios have different speeds).

4. Detection: Those with low m/z ratios and hence higher speeds will reach the detector first. A current is created when the positive ions hit the detector and this is measured along with the time of flight.

Mass Spectrum

Once the all of the ions present have detected a spectrum is created and then simplified into a graph with sticks, a little like a bar chart.

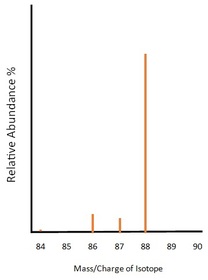
This spectrum is of the element Strontium. According to our spectrum strontium has four isotopes of mass 84, 86, 87 and 88 with percentage abundances of 0.56%, 9.86%, 7,00% and 82.58% respectively. The mass/charge numbers given are of the assumption that all of the ions have a +1 charge. Using this data, we can work out the relative molecular mass of the sample with great accuracy.

Working out the relative atomic mass

The relative atomic mass (RAM) of an element is given the symbol Ar and is defined as:

“The relative atomic mass of an element is the weighted average of the masses of the isotopes on a scale of which a carbon-12 atom has a mass of exactly 12 units.”

This kind of average allows us to take into account that each isotope has different amounts. Take out Strontium example:

If we take each mass number (once again assuming +1 charges), multiply them by their percentages and then add each one together, we can then divide them by 100 (because it is a percentage) to get the weighted average, or relative atomic mass of our sample. \[\frac{{(84×0.56) + (86×9.86) + (87×7.00) + (88×82.58)}}{{100}} = 87.71 \]