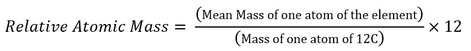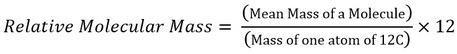Relative Atomic Mass (Ar)
The atoms in an element all have the same atomic number. The elements are arranged in order of increasing atomic number in the periodic table. The relative atomic mass of an element is usually shown in the top of its box in the periodic table, with the atomic number at the bottom. Some tables show this information the other way round. If you are not sure which number to use, the relative atomic mass will always be the larger number of the two.
The periodic tables used at GCSE show relative atomic masses as whole numbers (chlorine is a common exception at 35.5). The periodic table you use at this level shows relative atomic masses to one decimal place. So the Ar of H is 1.0 not 1, and the Ar of Fe is 55.8 not 56. Make sure you use the correct periodic table in your studies.
Relative Molecular Mass (Mr)
You can assume when writing formulae and equations that most elements exist as single atoms. This includes all the metals and the noble gases of Group 0. You need to take care with the other gaseous elements and the elements in Group 7. They exist as diatomic molecules with two atoms joined together by chemical bonds. This means for example that the formula of hydrogen gas is H2 not H, and the formula of chlorine gas is Cl2 not Cl.
You calculate the relative molecular mass of a substance by adding together the relative atomic masses of all the atoms in its formula. For example:
The formula of chlorine gas is Cl2.
The Ar of chlorine is 35.5 (from the Periodic Table).
The Mr of chlorine gas = 35.5 + 35.5 = 71.0
Note that you must give the answer to one decimal place.
You calculate the relative molecular mass of compounds by adding together the relative atomic masses of all the atoms in the formula. For example:
The formula of carbon dioxide is CO2
The Ar of carbon is 12.0 and the Ar of oxygen is 16.0
The Mr of carbon dioxide = 12.0 + 16.0 + 16.0 = 44.0
Remember that the formulae of compounds may have brackets in them. For example, Compounds and Mr the formula of magnesium hydroxide is Mg(OH)2. Where this happens, multiply the Ar of each atom inside the brackets by the number outside. For example:
The formula of magnesium hydroxide is Mg(OH)2
The Ar of Mg is 24.3, the Ar of O is 16.0 and the Ar of H is 1.0
The Mr of Mg(OH)2 = 24.3 + (2 × 16.0) + (2 × 1.0) = 24.3 + 32.0 + 2.0 = 58.3
Amount of Substance
It is important that you know the definitions of relative atomic mass Ar and relative molecular mass Mr.
Relative atomic mass, Ar (ALSO known as RAM): An element’s relative atomic mass is the mean mass of an atom of the element compared to one-twelfth the mass of a 12C atom.
Relative molecular mass, Mr (ALSO known as RMM) Relative molecular mass is the mean mass of a molecule compared to one-twelfth the mass of a 12C atom.
Avogadro’s Constant and the Mole
Chemists need to know the amount of each substance in a chemical reaction. This lets them calculate just how much of each reactant they need, and how much useful product is likely to be made. In everyday life, the amount of something is usually its mass in grams if it is solid, or its volume in cubic centimetres if it is a liquid or gas. Other measures might be used for bigger quantities, such as kilograms, tonnes, cubic metres, and so on. Chemists need to know how many atoms, molecules, and ions they have in a reaction. This is what a chemist means by the amount of a substance. This might seem difficult to find out, as atoms, molecules, and ions are incredibly small and have very little mass. This is where the concept of the mole helps.
The mole is the unit for amount of substance. It is given the symbol mol. The number of atoms in 12g of 12C is called the Avogadro constant, which is given the symbol L or NA. The Avogadro constant is 6.022 x 1023.
This is approximately six hundred thousand billion billion, a number that does not make much sense in everyday life. If you could stack the Avogadro number of £1 coins one on top of the other, the pile would reach from the Earth to the centre of the galaxy and back again – four times. The mole and Avogadro’s constant only make sense when applied to incredibly tiny particles with very little mass.
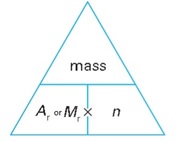
The mass of one mole of a substance is its Ar or Mr in grams. So one mole of 12C atoms has a mass of 12.0 g, and one mole of oxygen molecules O2 has a mass of 32.0 g. These two equations show how mass, relative mass, and amount of substance are related:
For atoms: mass = Ar x n
For molecules: mass = Mr x n
The symbol n represents the amount of substance in moles.
Worked Example using Ar: What is the mass of 3 mol of helium atoms, Ar = 4.0?
Mass = Ar x n
Mass = 4.0 x 3 = 12.0 g
Worked Example using Mr: What is the mass of 1.5 mol of nitrogen molecules, Mr = 28.0?
Mass = Mr x n
Mass = 28.0 x 1.5 = 42.0 g
You can also find the mass of ions if you know the relative formula mass and the amount of substance. Remember that the electron has 1836 times less mass than the proton, so you can ignore its mass when you work out the Mr of an ion.
For example:
The formula of the sulphate ion is SO42-
The Ar of sulfur is 32.1 and the Ar of oxygen is 16.0
The Mr of the sulfate ion = 32.1 + (4 x 16.0) 32.1 + 64.0 = 96.1
Worked Example: What is the mass of 2.0 mol of sulfate ions, Mr = 96.1?
mass = Mr x mol
mass = 96.1 x 2.0 = 192.2 g
Remember:
For atoms: mass = Ar x n
For molecules: mass = Mr x n
These equations can be re-arranged in two different ways. This lets you find one unknown quantity if you know the other two.
|
Here are a few more examples: How many moles of atoms are there in 27.0g of beryllium, Ar = 9.0. n = mass / Ar n= 27.0 / 9.0 n= 3.00 mol How many moles of molecules are there in 11.0g of carbon dioxide, Mr = 44.0? n = mass / Mr n = 11.0 / 44.0 n = 0.250 mol What is the relative formula mass of compound Y, if 0.5 mol has a mass of 20.0g? Mr = mass / n Mr = 20.0 / 0.5 Mr = 40.0 What is the relative atomic mass of element X, if 2.0 mol has a mass of 90.0g? Ar = mass / n Ar = 90.0 / 2.0 Ar = 45.0 |